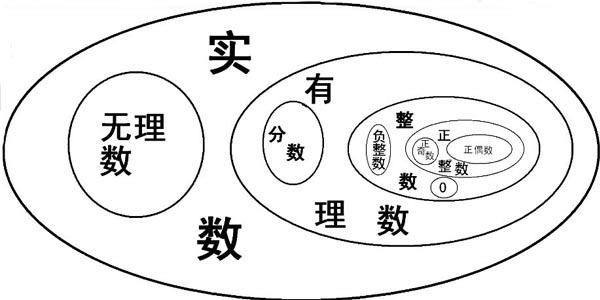
有理数与无理数的区别

有理数与无理数的区别

1、把有理数和无理数都写成小数形式时，有理数能写成有限小数和无限循环小数。

比如4=4.0, 4/5=0.8, 1/3=0.33333……而无理数只能写成无限不循环小数,

比如√2=1.414213562…………根据这一点,人们把无理数定义为无限不循环小数。

2、所有的有理数都可以写成两个整数之比；而无理数不能。

根据这一点，有人建议给无理数摘掉“无理”的帽子，把有理数改叫为“比数”，把无理数改叫为“非比数”。

3、有理数的位数是有限的，二无理数的位数是无限的。

扩展资料

有理数和无理数的和一定为无理数。

有理数可以化为两整数比(即分数)的形式，而无理数则不能。假设有理数a/b与无理数x的和是有理数c/d，其中a,b,c,d都是整数，且b,d不为零那么a/b+x=c/d, x=c/d-a/b=(bc-ad)/bdx可以化为两整数bc-ad和bd的比的形式。

x是有理数，这与题设x是无理数矛盾。所以一个有理数与一个无理数的和不能是有理数，一定为无理数。

参考资料来源：百度百科-有理数

参考资料来源：百度百科-无理数