什么是抽样误差?通过哪些方法可减小抽样误差?
的有关信息介绍如下:抽样误差是样本估计值与被推断的总体真实值之差。由用局部的样本统计量对整体的总体参数作出估计所引起的误差。它是一种随机误差,是由于偶然性因素产生的,不可避免。
抽样误差的大小具有一定的规律,研究和运用抽样误差的规律,是根据样本估计总体时必须的,也是统计分析的重要内容。
方法:抽样的随机误差与三个因素有关。
一是样本容量,样本容量越大,抽样误差越小,这个很好理解。在极端情况下,如果能进行普查,就不会有随机误差了。
二是抽样时是否分层,分层抽样能够降低抽样的随机误差。
三是抽样时是否分群,整群抽样会增加抽样的随机误差。
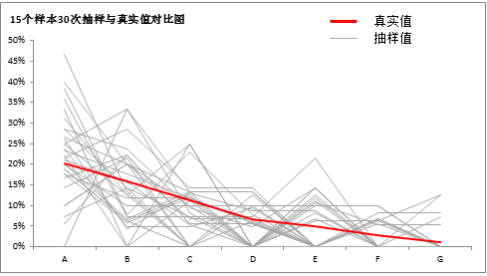
扩展资料
抽样误差的大小一般用标准误差衡量。
标准误差(英文:Standard Error),即样本统计量(平均值)的标准差(英文:Standard Deviation),是描述对应的样本统计量抽样分布的离散程度及衡量对应样本统计量抽样误差大小的尺度。
对一个总体多次抽样,每次样本大小都为n,那么每个样本都有自己的平均值,这些平均值的标准差叫做标准误差。标准差是单次抽样得到的,用单次抽样得到的标准差可以估计多次抽样才能得到的标准误差。
随着样本数(或测量次数)n的增大,标准差趋向某个稳定值,即样本标准差s越接近总体标准差σ,而标准误差则随着样本数(或测量次数)n的增大逐渐减小,即样本平均数越接近总体平均数μ、
故在实验中也经常采用适当增加样本数(或测量次数)使n增大的方法来减小实验误差,但样本数太大意义也不大。标准差是最常用的统计量,一般用于表示一组样本变量的分散程度。
标准误差一般用于统计推断中,主要包括假设检验和参数估计,如样本平均数的假设检验、参数的区间估计与点估计等。
参考资料来源:百度百科-抽样误差



