线性规划问题的解题步骤

线性规划问题的解题步骤

解决简单线性规划问题的方法是图解法，即借助直线（线性目标函数看作斜率确定的一族平行直线）与平面区域（可行域）有交点时，直线在y轴上的截距的最大值或最小值求解，它的步骤如下：

（1）设出未知数，确定目标函数。

（2）确定线性约束条件，并在直角坐标系中画出对应的平面区域，即可行域。

（3）由目标函数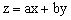变形为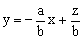，所以求z的最值可看成是求直线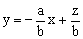在y轴上截距的最值（其中a、b是常数，z随x、y的变化而变化）。

（4）作平行线：将直线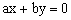平移（即作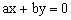的平行线），使直线与可行域有交点，且观察在可行域中使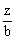最大（或最小）时所经过的点，求出该点的坐标。

（5）求出最优解：将（4）中求出的坐标代入目标函数，从而求出z的最大（小）值。

扩展资料：

线性规划基本概念：

（1）可行解：把满足约束条件的一组决策变量值 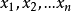 称为该线性规划问题的可行解。

（2）可行解集/可行解域：满足约束条件的可行解的全体称为可行解集，在平面上，所有可行解的点的集合称为可行解域。

（3）最优解：在可行解集中，使目标函数达到最优值的可行解称为最优解。

参考资料：

百度百科-线性规划