世纪金榜数学选修2-3答案解析
的有关信息介绍如下:第一题:
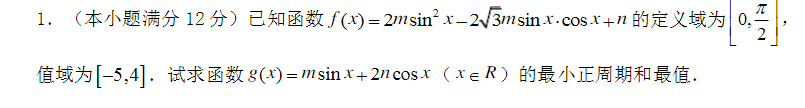
答案:

第二题:

答案:


第三题:

答案:

第四题:

答案:


这部分内容主要考察的是偶函数的知识点:
如果对于函数f(x)的定义域内任意的一个x,都有f(x)=f(-x),那么函数f(x)是偶函数(Even Function)。
如果知道函数表达式,对于函数f(x)的定义域内任意一个x,都满足 f(x)=f(-x) 如y=x*x;如果知道图像,偶函数图象关于y轴(直线x=0)对称,定义域D关于原点对称是这个函数成为偶函数的必要不充分条件。
代数判断法,主要是根据奇偶函数的定义,先判断定义域是否关于原点对称,若不对称,即为非奇非偶,若对称,f(-x)=-f(x)的是奇函数; f(-x)=f(x)的是偶函数。
奇函数一定满足f(0)=0(因为F(0)这个表达式表示0在定义域范围内,F(0)就必须为0)所以不一定奇函数有f(0),但有F(0)时F(0)必须等于0,不一定有f(0)=0,推出奇函数,此时函数不一定为奇函数,例f(x)=x^2。
定义在R上的奇函数f(x)必满足f(0)=0;因为定义域在R上,所以在x=0点存在f(0),要想关于原点对称,在原点又只能去一个y值,只能是f(0)=0。这是一条可以直接用的结论:当x可以取0,f(x)又是奇函数时,f(0)=0)。
当且仅当f(x)=0(定义域关于原点对称)时,f(x)既是奇函数又是偶函数。在对称区间上,被积函数为奇函数的定积分为零。

