三角形的中线怎么求

三角形的中线怎么求

三角形一条中线两侧所对边平方和等于底边的一半平方与该边中线平方的和的2倍。

即，对任意三角形△ABC，设是I线段BC的中点，AI为中线，则有如下关系：

AB^2+AC^2=2BI^2+2AI^2

或作AB^2+AC^2=  (BC)^2+2AI^2

通过两式相减，还可以得到|AB^2-AC^2|=2BC*IH。 （H为垂足）

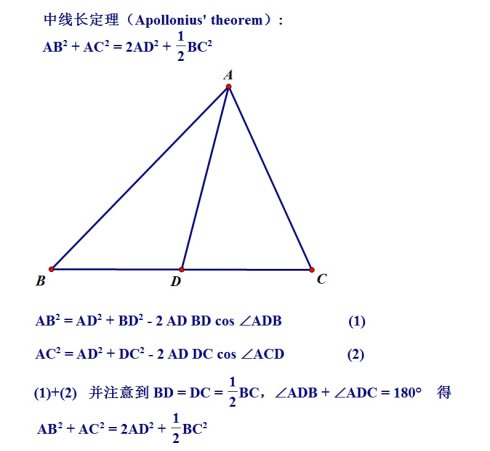
扩展资料：

中线定理即为斯台沃特定理在中点时的结论，可由斯台沃特定理直接得出，但是斯台沃特定理不容易理解。下面有四种比较容易理解的方法。

特殊点、线：五心、四圆、三点、一线：这些是三角形的全部特殊点，以及基于这些特殊点的相关几何图形。“五心”指重心、垂心、内心、外心和旁心；“四圆”为内切圆、外接圆、旁切圆和欧拉圆；“三点”是勒莫恩点、奈格尔点和欧拉点；“一线”即欧拉线。

三角形的稳定性使其不像四边形那样易于变形，有着稳定、坚固、耐压的特点。三角形的结构在工程上有着广泛的应用。许多建筑都是三角形的结构，如：埃菲尔铁塔，埃及金字塔等等。

参考资料：百度百科---中线定理