向量平行公式

向量平行公式

两个向量a,b平行：a=λb （b不是零向量）；两个向量垂直：数量积为0,即　a•b=0。枯念

坐标表示：a=(x1,y1),b=(x2,y2)

a//b当且仅当x1y2-x2y1=0

a⊥b当且仅当x1x2+y1y2=0

在直角坐标系内，我们分别取与滚哗x轴、y轴方向相同的两个单位向量i、j作为基底。任作一个向量a，由平面向量基本定理可知，有且只有一对实数x、y，使得：a=xi+yj，我们把(x,y)叫做向量a的（直角）坐标，记作：a=(x,y)。

其中x叫做a在x轴上的坐标，y叫做a在y轴上的坐标，上式叫做向量的大败行坐标表示。在平面直角坐标系内，每一个平面向量都可以用一对实数唯一表示。

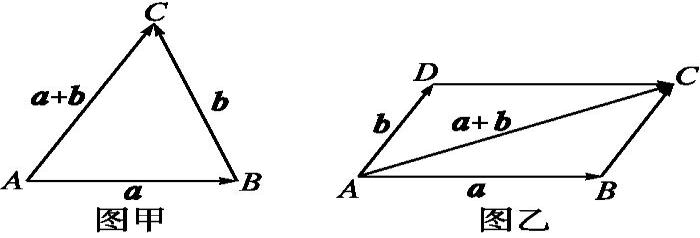
扩展资料：

如果e1和e2是同一平面内的两个不共线的非零向量，那么对该平面内的任一向量a，有且只有一对实数λ、μ，使a= λe1+ μe2。

给定空间三向量a、b、c，向量a、b的向量积a×b，再和向量c作数量积(a×b)·c，所得的数叫做三向量a、b、c的混合积，记作(a,b,c)或(abc)，即(abc)=(a,b,c)=(a×b)·c

混合积具有下列性质：

1、三个不共面向量a、b、c的混合积的绝对值等于以a、b、c为棱的平行六面体的体积V，并且当a、b、c构成右手系时混合积是正数；当a、b、c构成左手系时，混合积是负数，即(abc)=εV（当a、b、c构成右手系时ε=1；当a、b、c构成左手系时ε=-1）

2、上条性质的推论：三向量a、b、c共面的充要条件是(abc)=0

3、(abc) = (bca) = (cab) = - (bac) = - (cba) = - (acb)

参考资料：百度百科——平面向量