什么是傅里叶函数
的有关信息介绍如下:
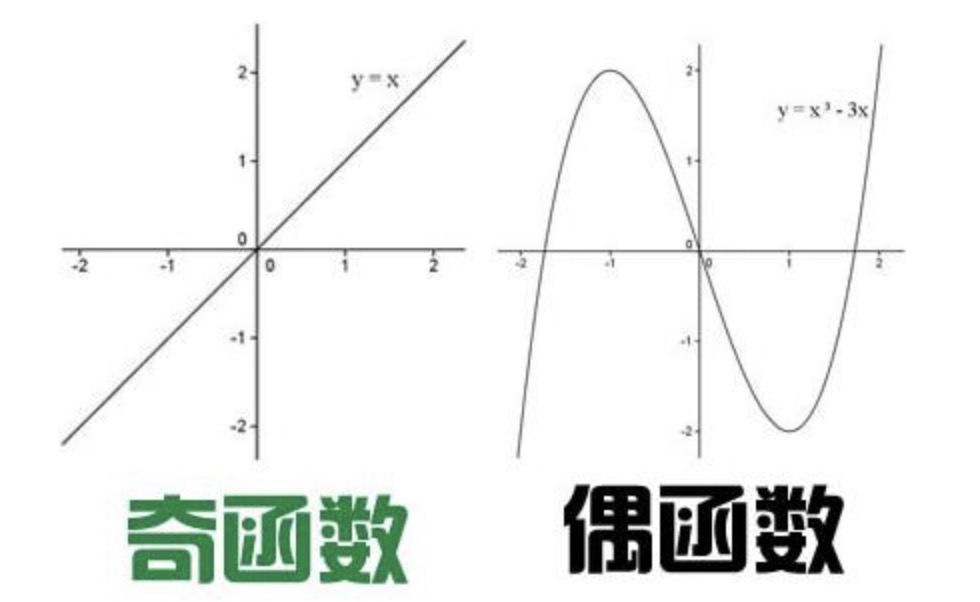
法国数学家傅里叶发现,任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示(选择正弦函数与余弦函数作为基函数是因为它们是正交的),后世称为傅里叶级数(法文:série de Fourier,或译为傅里叶级数)一种特殊的三角级数。目录傅里叶级数傅里叶级数的公式傅里叶级数的收敛性三角函数族的正交性奇函数和偶函数广义傅里叶级数 编辑本段傅里叶级数 Fourier series 一种特殊的三角级数。法国数学家J.-B.-J.傅里叶在研究偏微分方程的边值问题时提出。从而极大地推动了偏微分方程理论的发展。在中国,程民德最早系统研究多元三角级数与多元傅里叶级数。他首先证明 傅里叶级数多元三角级数球形和的唯一性定理,并揭示了多元傅里叶级数的里斯 - 博赫纳球形平均的许多特性。傅里叶级数曾极大地推动了偏微分方程理论的发展。在数学物理以及工程中都具有重要的应用。 ============================================================================================================编辑本段傅里叶级数的公式 给定一个周期为T的函数x(t),那么它可以表示为无穷级数: (j为虚数单位)(1) 其中,可以按下式计算: 傅里叶级数(2) 注意到是周期为T的函数,故k 取不同值时的周期信号具有谐波关系(即它们都具有一个共同周期T)。k=0时,(1)式中对应的这一项称为直流分量,时具有基波频率,称为一次谐波或基波,类似的有二次谐波,三次谐波等等。编辑本段傅里叶级数的收敛性 傅里叶级数的收敛性:满足狄利赫里条件的周期函数表示成的傅里叶级数都收敛。狄利赫里条件如下: 在任何周期内,x(t)须绝对可积; 傅里叶级数在任一有限区间中,x(t)只能取有限个最大值或最小值; 在任何有限区间上,x(t)只能有有限个第一类间断点。 吉布斯现象:在x(t)的不可导点上,如果我们只取(1)式右边的无穷级数中的有限项作和X(t),那么X(t)在这些点上会有起伏。一个简单的例子是方波信号。编辑本段三角函数族的正交性 所谓的两个不同向量正交是指它们的内积为0,这也就意味着这两个向量之间没有任何相关性,例如,在三维欧氏空间中,互相垂直的向量之间是正交的。事实上,正交是垂直在数学上的的一种抽象化和一般化。一组n个互相正交的向量必然是线形无关的,所以必然可以张成一个n维空间,也就是说,空间中的任何一个向量可以用它们来线形表出。三角函数族的正交性用公式表示出来就是: 傅里叶级数 编辑本段奇函数和偶函数 奇函数可以表示为正弦级数,而偶函数则可以表示成余弦级数: 傅里叶级数 只要注意到欧拉公式: ,这些公式便可以很容易从上面傅里叶级数的公式中导出。编辑本段广义傅里叶级数 任何正交函数系,如果定义在[a,b]上的函数f(x)只具有有限个第一类间断点,那么如果f(x)满足封闭性方程: (4), 那么级数 (5) 必然收敛于f(x),其中: (6)。 傅里叶级数事实上,无论(5)时是否收敛,我们总有: 成立,这称作贝塞尔(Bessel)不等式。此外,式(6)是很容易由正交性推出的,因为对于任意的单位正交基,向量x在上的投影总为 。