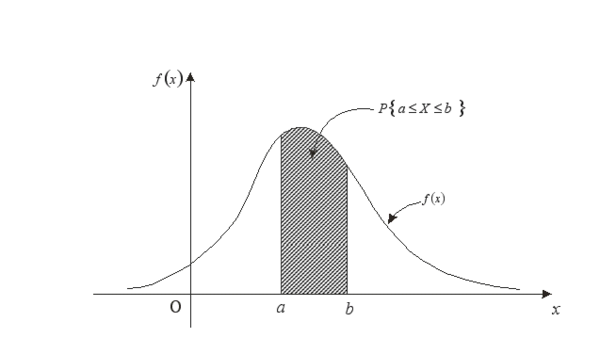
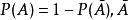概率计算公式
的有关信息介绍如下:概率公式
P(A)=构成事件A样本数目整个样本空间S的样本数目P(A)=构成事件A样本数目整个样本空间S的样本数目。
公理1:0≤P(A)≤10≤P(A)≤1既P(A)是一个0到1之间的非负实数。
公理2:P(S)=1P(S)=1整个样本空间的概率值为1。
公理3:P(A⋃B)=P(A)+P(B)P(A⋃B)=P(A)+P(B)如果AB互斥。

定理1:(互补法则):P(A¯¯¯¯)=1−P(A)P(A¯)=1−P(A)。
定理2:P(∅∅)=0。
定理3:P(A1⋂A2…⋂An)=∑nj=1P(Aj)P(A1⋂A2…⋂An)=∑j=1nP(Aj)。
定理4:P(A∖B)=P(A)−P(A⋂B)(P(A∖B)A−B,也就是AB是差集关系)P(A∖B)=P(A)−P(A⋂B)(P(A∖B)A−B,也就是AB是差集关系)。
定理5:P(A⋃B)=P(A)+P(B)−P(A⋂B)P(A⋃B)=P(A)+P(B)−P(A⋂B)。
定理6:P(A⋂B)=P(A)×P(B|A)=P(B)×P(A|B)(P(B|A)表示在B发生的情况下发生A的概率)。P(A⋂B)=P(A)×P(B|A)=P(B)×P(A|B)(P(B|A)表示在B发生的情况下发生A的概率)。
定理7:P(A⋂B)=P(A)×P(B)P(A⋂B)=P(A)×P(B)。
贝叶斯公式:P(A|B)=P(B|A)×P(A)P(B)P(A|B)=P(B|A)×P(A)P(B)。
全概率公式:P(B)=∑ni=1P(Ai)×P(B|Ai)P(B)=∑i=1nP(Ai)×P(B|Ai)。
期望:E(x)=∑ni=1P(xi)×xi。